
Is strong AI inevitable?
Don’t speculate. Don’t yield to experts. Look for yourself.
Any question about the future is susceptible to unknown unknowns, futile speculations about things undiscovered. We need examples we can observe and interrogate now. While we don’t have strong AI, we do have rigorous examples of weak and strong intelligence. A comparison of the nature of knowledge in its weak and strong forms offers a penetrating and non-technical look into the prospects for strong AI.
Our last stop on this tour of the AI landscape introduced induction as the prevailing theory of knowledge creation, and the central role that explanations play in workable inductive systems. Here, I’ll apply that framework to shed some light on one of the most contentious and important debates in AI: Are we on the path to artificial general intelligence? Is tomorrow’s strong AI the inevitable extension of today’s weaker examples?
Here’s the plan: We’ll examine two points along the knowledge hierarchy, one associated with weak AI, the other a much stronger form. I’ve labelled these points predictions and explanations, respectively, and I’ll make these terms more precise as we go. Through concrete examples, you can evaluate the quality of each intelligence yourself, and decide whether the path from weak to strong seems smooth and incremental, or perilous and disjoint.
Possible is not inevitable
Before we dive in, there’s one aspect of this debate we should set aside, the difference between possible and inevitable. There’s a reasonable expectation that strong AI is physically possible. The physicist and pioneer of quantum computing David Deutsch provides a rich discussion of that possibility in The Fabric of Reality. The claim to possibility is grounded in the Turing principle: “There exists an abstract universal computer whose repertoire includes any computation that any physically possible object can perform.” Life embodies intelligence. The Turing principle says that a computer could be tractably built and programmed to render any physical embodiment, including objects such as intelligence-producing brains. The possibility of strong AI follows logically from the Turing principle, which Deutsch maintains is so widely accepted as to be pragmatically true.
“The Turing principle guarantees that a computer can do everything a brain can do. That is of course true, but it is an answer in terms of prediction, and the problem is one of explanation.” David Deutsch
Despite this principled argument, the inevitability of AI remains a hotly contested topic among philosophers, scientists and mathematicians (Roger Penrose being a particularly formidable critic). However, the disagreements are rooted less in theoretical arguments as in the specific “how do we get there from here” implications. Deutsch explains, “It is then not good enough for artificial-intelligence enthusiasts to respond brusquely that the Turing principle guarantees that a computer can do everything a brain can do. That is of course true, but it is an answer in terms of prediction, and the problem is one of explanation. There is an explanatory gap.”
To assess the inevitability of AI, we need to illuminate the explanatory gaps between weak and strong forms of intelligence.
When everything is prediction
One last bit of housekeeping. For some, the inevitability of AI is not only an answer in terms of prediction, prediction is the essence of intelligence itself. This is patently untrue. Intelligence is like Whitman, “I am large, I contain multitudes.” But it’s the law of the hammer to treat everything as if it were a nail. So motivated, any functional gap in AI may be framed as a prediction problem: The crux of the AI problem is prediction under uncertainty; reasoning entails activities of prediction; predicting general rules as common sense; and so on.
When everything is rooted in prediction, including the goal, every open problem appears incremental. Frequently, arguments for inevitability reference the indirect factors of production in prediction engines, such as the pace of investment and increases in people, computing resources and data. This is the tweet-sized version of the AI roadmap: Prediction is a unit of intelligence. To achieve greater intelligence, just add more prediction resources.
In a recent article for Harvard Business Review, one of the most influential AI researchers Andrew Ng offers this rule of thumb: “If a typical person can do a mental task with less than one second of thought, we can probably automate it using AI either now or in the near future.” Data and the talent to expertly apply the software are the only scarce resources impeding progress for these one-second tasks. To be fair, Ng cuts through the hype, acknowledging that “there may well be a breakthrough that makes higher levels of intelligence possible, but there is still no clear path yet to this goal.”
The tendency to conflate lower order capabilities like predictions with more sophisticated forms of intelligence is not limited to sloppy talk in business and marketing forums. It extends deep into the technical domains of statistics and machine learning.
The statistician Galit Shmueli explains how the conflation of prediction and explanation has reached epidemic proportions, due to the indiscriminate use of statistical modeling. “While this distinction has been recognized in the philosophy of science, the statistical literature lacks a thorough discussion of the many differences that arise in the process of modeling for an explanatory versus a predictive goal.” For many, explanation has come to mean “efficient” or “interpretable” prediction.
Consider this example from the University of Washington, explaining the predictions of any classifier. “By ‘explaining a prediction’, we mean presenting textual or visual artifacts that provide qualitative understanding of the relationship between the instance’s components (e.g. words in text, patches in an image) and the model’s prediction.” The “explanation” is a human interpretable description derived from the more complex model.
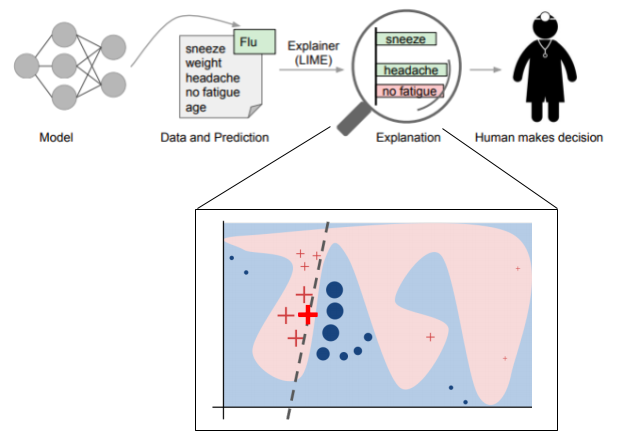
It’s an elegant solution for making complex models more interpretable, but as we’ll see, it’s a far cry from explanations in the more rigorous scientific sense of the term. Tellingly, Ng and his collaborators leveraged this approach for “explaining predictions” in a recent paper.
We don’t care about wordplay, we want to understand the substance of the thing. And whatever we call it, we need to determine whether something substantial separates the products of strong and weak intelligence. To do that, we’ll look in more detail at predictions, as associated with machine learning, and explanations, as associated with scientific discovery.
Weak Intelligence: Prediction engines
This is my dog Thor. His sense of smell is orders of magnitude better than mine. He hears sounds at frequencies 20,000 Hz above my upper limit. Thor perceives the world in a way that I could never apprehend. He builds remarkably versatile predictive models. He learns through positive and negative reinforcement (liver treats and time-outs, respectively). He frequently surprises me, when I can’t hear what he hears or smell what he smells. Yet he never, ever, explains. When Thor’s world changes, he doesn’t ask why.

Despite our inability to have deep conversations, I’ve come to love Thor. And I feel the same way about my other go-to prediction engine, the navigation app in my phone. It frequently delights me, routing me through traffic in ways I’ve never travelled before. Like Thor, the app is powered by a torrent of data beyond my senses, rapidly building and updating its directions. As explained on Google’s AI blog, “In order to provide the best experience for our users, this information has to constantly mirror an ever-changing world.” But it never offers any higher order explanation of traffic that reaches beyond its senses.
Proponents of prediction may cry foul. “These are your examples of prediction, a navigation app and your dog?!” Again, keep in mind that I’m only trying to locate a plateau of weak intelligence, such that we can contrast it with the stronger forms that follow. In that spirit, we need to set a boundary.
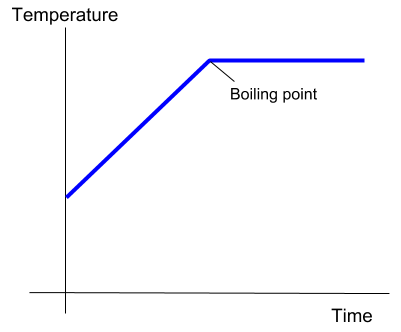
Peeking under the hood, the nature of predictions is revealed in their boundaries. Brett Hall offers a simple illustration, a pot of boiling water. The temperature of the water increases steadily until the boiling point. Based on observations before the boiling point, it would be quite reasonable to predict the temperature will continue to rise. But once the temperature exceeds the boiling point, it defies prediction and demands explanation. Hall wryly asks, if extrapolation fails even when applied to this simple system, how can it be expected to succeed when things are more complicated?
You may be thinking, this is a toy model applied to a complex system. It’s bound to fail. Just give it more data and a more robust model! This is a fair criticism, as the entire premise of the incremental roadmap is that we can continue to ingest new data to create evermore sophisticated systems.
So let’s adopt the most idealized concept of a prediction engine we can imagine, an oracle with godlike powers of divination. You can ask the oracle whatever you want and it will predict what will happen. Of course, cash being king, you ask it to predict stock prices. And it works! You invest small amounts of money in stocks predicted to rise, and your investments increase. (Curiously, you notice a slight discrepancy between the predicted values and the actual stock prices, but you think nothing of it at the time.)
Gradually, the size and pace of your investments increase, as does your influence and reputation. Now, you’re not only playing the markets, you’re moving them! But strangely, your oracle begins to fail you. Those discrepancies between the predicted and actual prices are now quite pronounced, frequently undermining your investments. Your oracle’s predictions have degraded to approximations. It still describes the system, but it can’t tell you the impact of your interventions on that system, without moving you inside the model.
These features encapsulate what the political scientist Eugene Meehan called the system paradigm of explanation. He described explanations as empirical generalizations, formalized in models such as Bayesian networks and structural equations. Predicted outcomes are insufficient. Observations cannot simply fit the model, for a model can be created to fit any set of facts or data. If the system sufficiently reflects the environment, the prediction applies; if it doesn’t, the prediction fails. This is what it means to “mirror an ever-changing world.” And this problem is endemic to the task of prediction.
Implicitly, the system paradigm of explanation is what many people associate with prediction engines and the incremental path to improve them. However, as an exemplar of strong AI, we can do better.
Strong Intelligence: Scientific explanations
I’ve argued previously that science, our most successful knowledge creating institution, is an exemplar for artificial intelligence. With that in mind, I’ll surface examples that illustrate the scientific conception of explanations. As compared with prediction, these examples encompass a range of important differences, in form, function, reach and integration. I’ll also use one of the best scientific explanations, quantum mechanics, to illuminate these differences. If AI begins automating this quality of scientific discovery, we’ll all most certainly agree it’s strong indeed.
But fittingly, let’s start with a sunrise. For a very long time, we believed the sun rises because we observe it. But now we understand it in terms of the functioning of the solar system and the laws of physics. Explaining is much more robust than predicting. We know the sun is rising even when it’s cloudy. If we were orbiting the planet, frequent sunrises would not be at all surprising. (They would, however, remain awe-inspiring!) Appearances notwithstanding, we know in reality that the sun isn’t rising at all.

Let’s pause for a moment to behold this explained sunrise. There’s a profound distance between our observations of the sunrise and its explanation. The observations appear regular and uniform. Every morning the sun rises in the east. Yet the deeper explanation of the sunrise permits unobservable data, such as what’s happening when the sun is obscured by the clouds. It even admits the imagination, the counterfactual case of observers in orbit.
In his discussion of the complexity of scientific inference, the philosopher Wesley Salmon used this example to characterize predictions based on “crude induction” as “unquestionably prescientific”, even the antithesis of scientific explanations. Explanations sit at the apex of the knowledge hierarchy due to their depth and reach. “A scientific theory that merely summarized what had already been observed would not deserve to be called a theory.” Here in the scientific milieu, the illusion of induction is laid bare. Contrary to the idea that knowledge is induced from data, science reveals a rich integration of explanations that predicts otherwise unobservable data.
Let’s look under the hood of explanations, as we did with predictions. Explanations (or theories) consist of interpretations of how the world works and why. These explanations are expressed in formalisms as mathematical or logical models. Models provide the foundation for predictions, which in turn provide the means for testing through controlled experiments.
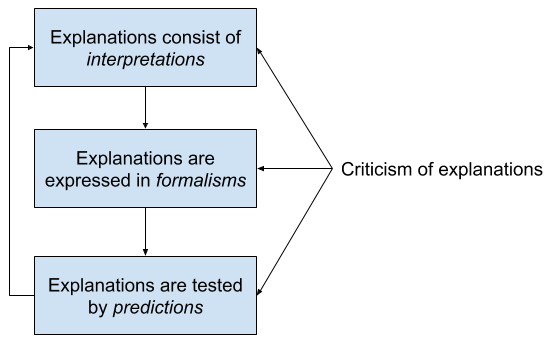
In this schema, explanations are the unity of interpretations, formalisms and predictions. Each component serves a functional role and each maystand-alone. Iteratively, explanations may be tested via their predictions, and their results may draw attention to explanatory gaps in need of attention. But their unifying purpose is to elucidate and criticize the explanations. In this light, predictions (a part) is subsumed by explanations (the whole). Explanations behave more like living ecosystems than static artifacts, a dynamic churn of conjecture, predictions, experimentation, and criticism.
The complex nature of scientific explanations finds rich expression in quantum mechanics. There’s a risk that this example is more complicated than the thing I’m trying to explain. But this is also one of the most robust and counter-intuitive explanations in science. It truly captures the nature of alien-like superintelligence, our expectation of strong AI. Even grossly simplified, it serves our purpose here, as a peak of strong intelligence.
The formalisms of quantum mechanics may be used for prediction without any interpretation of the underlying physical reality. Yet there’s a wide range of competing interpretations, such as collapsing waves, pilot waves, many worlds, or many minds, to name but a few. And critically, these interpretations matter. They inspire researchers, influence research programs and contribute to the production of futureknowledge.
Going a little deeper, consider the distinction between laws that precisely describe observations (phenomena), and explanations that have the reach and power to create those laws. The philosopher Nancy Cartwright, in her influential book, How the Laws of Physics Lie, highlights the difference between a generalized account capable of subsuming many observations (phenomenological laws), and the specificity needed for models to actually predict the real world. “The route from theory to reality is from theory to model, and then from model to phenomenological law. The phenomenological laws are indeed true of the objects in reality — or might be; but the fundamental laws are true only of objects in the model.”
So again, to appreciate how profoundly different scientific explanations are from predictions, let’s return to the example of quantum mechanics. There’s a generalized theory of how a system will change (formalized in Schrödinger’s equation) and the specific energies acting on the system (formalized as the Hamiltonian operator set up for the system). Cartwright explains, “It is true that the Schrödinger equation tells how a quantum system evolves subject to the Hamiltonian; but to do quantum mechanics, one has to know how to pick the Hamiltonian.”
Just like our sunrise, quantum theory spans a rich hierarchy of explanations, not data, extending from generalized concepts to more specific models capable of actually predicting outcomes.
Inductive systems deal with structure, too, such as the hierarchy of features that compose an image. But here, we’re talking about structures that don’t just describe or represent data, but rather explain their underlying causes. These integrations form a lattice that supports the whole edifice, extending all the way down to language itself as primitive explanations. Just as reality exists across compounding tiers of abstraction, explanations need the support of other explanations. And frequently, explanations stand quite removed from data and observations. Like some mind-body duality, this unity is the content of knowledge itself.
Is strong AI inevitable?
We now have two distinct vantage points, the weaker plateau of predictions and the stronger peak of scientific explanations. So off we go from one to the other, on our trek to answer the question.
The first impediment on our path is the gap of interventions. To predict is to infer new observations beyond what we’ve observed thus far. Predictions are bounded by an assumption of uniformity. If the system changes, new data are needed to build a more accurate model. A model is less valuable if it’s merely descriptive. We want predictions we can act on, to buy a stock or treat a disease. But intervening entails changing the system, breaking the assumption of uniformity.
“God asked for the facts, and they replied with explanations.” Judea Pearl
So how wide is the gap of interventions? Judea Pearl is a pioneer of modern AI and probabilistic reasoning. In The Book of Why, he places associative predictions on the lowest rung of intelligence; interventions and more imaginative counterfactual reasoning as stronger forms. Pearl explains why this higher order knowledge cannot be created from the probabilistic associations that characterize inductive systems. As one of the originators of the idea, he’s now “embarrassed” by the claim that probabilities comprise a language of causation and higher order knowledge. Suffice it say the gap of interventions is at best spanned by a rickety bridge that not even Indiana Jones would cross without pause. But we troddle on.
Eventually we arrive at even more imposing barrier, the cliff of data. While interventions pose a significant gap along our path, they’re nothing compared to this impediment. The fuel of inductive systems is data. Scientific conjectures are often described as leaps of imagination. The “data” of imagination, counterfactuals, are by definition not observed facts! Quite unlike data, knowledge is composed of a rich lattice of mutually supporting explanations. When I try to reconcile the enthusiasm for data-driven technologies with the reality of conjectural knowledge, I’m reminded of Wile E. Coyote running off the cliff. What’s holding him up?

In his critical appraisal of deep learning, the scientist and AI researcher Gary Marcus claims deep learning may be hitting a wall (or perhaps falling off the cliff). He surveys many of the topics discussed in this post, such as the law of the hammer, the over-reliance on data, the limits of extrapolation, the challenges imposed by interventional and counterfactual reasoning, the “hermeneutic” nature of these self-contained and isolated systems and their limited ability to transfer knowledge.
Proponents of deep learning continue to defend their positionvigorously. But this perception that AI is hitting a wall is forcing a rethink on the prospects for inductive systems. Taking the pulse of the community and some notable unmet expectations, the AI researcher Filip Piękniewski argues that disillusionment, not strong AI, is the only inevitable outcome.
Much like Pearl, Marcus envisions a future that combines elements of explanatory knowledge with induction. “The right move today may be to integrate deep learning, which excels at perceptual classification, with symbolic systems, which excel at inference and abstraction.” This is undoubtedly true. Explanatory power is already deployed in the methodologies of machine learning, as in the selection of data, the choice of assumptions that bias learning algorithms, and the background knowledge used to “prime the pump” of induction.
But these are just observations from experts. You already know this. You know that reality frequently defies your assumptions of uniformity and foils your best laid plans. You don’t just observe a sunrise, you know why it rises. You’ve even unpacked the rich explanatory structure of quantum mechanics. You know that the most advanced inductive systems produce only pre-scientific knowledge, crude by the standards of our best scientific explanations.
And so you can answer for yourself: Will the gaps between weak and strong intelligence be crossed in predictable incremental steps or bold conjectural leaps?
In my estimation, all the impediments to strong AI are dwarfed by the instrumental fascination with inductive systems. Inductive systems like deep learning are powerful tools. It’s entirely understandable, even expected, that we should start with their practical uses. When heat engines were invented at the start of the industrial revolution, the initial interest was in their practical applications. But gradually, over 100 years, this instrumental view gave way to a much deeper theoretical understanding of heat and thermodynamics. These explanations eventually found their way into almost every modern-day branch of science, including quantum theory. The tool gave us heat engines; explanations gave us the modern world. That difference is truly breathtaking.
AI will follow the same progression, from these first practical applications to a deep theoretical understanding of knowledge creation. I hope it doesn’t take 100 years. But when it happens, strong AI will follow. Inevitably.
Cartwright, N. (1983). How the laws of physics lie. Clarendon Press.
Deutsch, D. (1998). The fabric of reality. Penguin.
Hall, B. (2017). Induction. http://www.bretthall.org/blog/induction
Marcus, G. (2018). Deep learning: a critical appraisal https://arxiv.org/abs/1801.00631
Marcus, G. (2018). In defense of skepticism about deep learning. https://medium.com/@GaryMarcus/in-defense-of-skepticism-about-deep-learning-6e8bfd5ae0f1
Meehan, E.J. (1968). Explanation in social science; a system paradigm. Dorsey Press
Pearl, J. & Mackenzie, D. (2018). The book of why: the new science of cause and effect. Basic Books
Piękniewski, F. (2018). AI winter is well on its way. https://blog.piekniewski.info/2018/05/28/ai-winter-is-well-on-its-way/
Ribeiro, M.T., Singh, S. & Guestrin, C. (2016). “Why should I trust you?”: Explaining the predictions of any classifier https://arxiv.org/abs/1602.04938
Salmon, W.C. (1967). The foundations of scientific inference. University of Pittsburgh Press.
Shmueli, G. (2010). To explain or to predict? Statistical Science, 25(3), 289–310. https://projecteuclid.org/euclid.ss/1294167961
